Data-Driven Optimization Techniques
In many scientific, engineering, and industrial contexts, we are faced with optimization problems where the objective function and constraints (if present) are not given via closed-form mathematical expressions, i.e., they are black-box. Instead, they are only accessible by running expensive evaluations, e.g., experiments and/or simulations. These problems arise in applications such as complex systems design, and control, where the target systems contain different and interacting physical mechanisms (electrical, mechanical, biological, analog/digital interfaces, etc.). To find the best (feasible) solution to this class of optimization problems, existing approaches try to trade off between exploitation (using information on the current best to improve on it), and exploration (acquiring information around the search space to find better solutions). In the recent years, there has been a rise of model-based approaches in which a surrogate model is built from the samples taken so far, which is then used to choose the next sampling point. However, the most popular methods in the state-of-the-art are still faced with practical problems such as iteration-based optimization performance and computational burden.
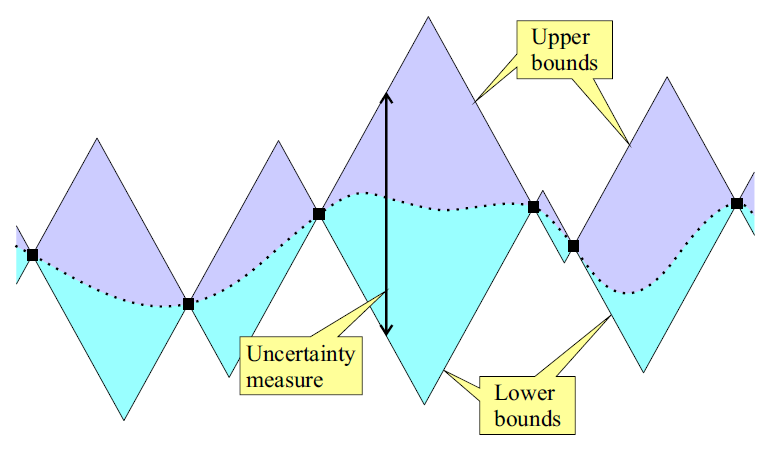
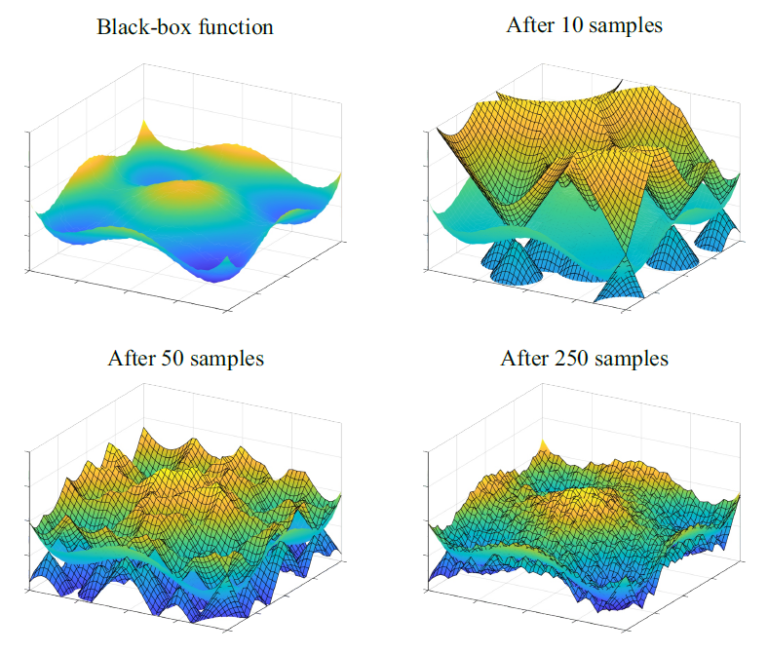
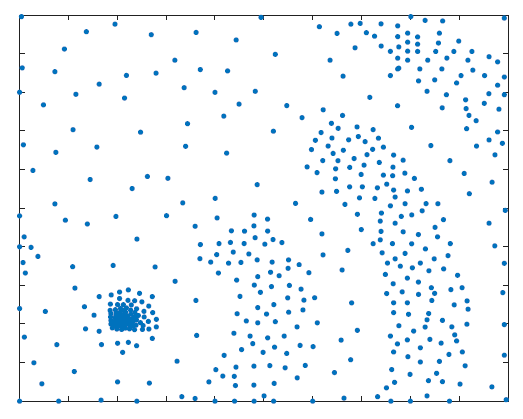
At SAS-Lab, we conduct research on black-box (otherwise referred as global or data-driven) optimization techniques which are iteration-efficient, and computationally light. We use Set Membership approaches to build a simple surrogate model of the underlying objective and constraint functions, and formulate an algorithm that automatically trades-off between exploitation, exploration, and safety with respect to constraint/s satisfaction. This has resulted in the Set Membership Global Optimization (SMGO), with competitive iteration-based optimization performance, guaranteed convergence properties, and much lighter computational burden compared to the state of the art. SMGO has been used in challenging case studies, and is available as an open-source toolbox in MATLAB File Exchange.
References
2022
SMGO-Δ: Balancing caution and reward in global optimization with black-box constraints Journal Article
In: Information Sciences, vol. 605, pp. 15-42, 2022, ISSN: 0020-0255.
2021
SMGO: A set membership approach to data-driven global optimization Journal Article
In: Automatica, vol. 133, pp. 109890, 2021.